kolmiot voivat vaikuttaa yksinkertaisilta luvuilta, mutta niiden taustalla oleva matematiikka on sen verran syvää, että sitä voidaan pitää omana subjektinaan: trigonometriana.

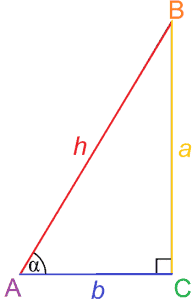
kuten nimestä voi päätellä, Trigonometria on kolmioiden tutkimista. Tarkemmin trigonometria käsittelee Kulmien ja sivujen välisiä suhteita kolmioissa.

hieman yllättäen trigonometriset suhdeluvut voivat antaa myös rikkaamman käsityksen ympyröistä. Näitä suhdelukuja käytetään usein laskennassa sekä monissa tieteenaloissa, mukaan lukien fysiikka, tekniikka ja tähtitiede.

tämän oppaan resurssit kattavat trigonometrian perusteet, mukaan lukien trigonometristen suhdelukujen ja funktioiden määrittelyn. Sitten he käyvät läpi, miten näitä toimintoja käytetään ongelmissa ja miten niitä havainnollistetaan.

tämän resurssioppaan lopuksi kerrotaan yleisimmät trigonometriset identiteetit.

Perustrigonometria

Trigonometria käsittelee erityisesti suorakulmaisen kolmion sivujen suhteita, joiden avulla voidaan määrittää kulman mitta. Näitä suhdelukuja kutsutaan trigonometrisiksi funktioiksi, ja alkeellisimmat ovat sini ja kosini.

näiden kahden funktion avulla määritellään muut tunnetut trigonometriset funktiot: tangentti, sekantti, kosekantti ja kotangentti.

Tämä osio alkaa käymällä läpi oikeuskolmioita ja selittämällä trigonometristen perusfunktioiden. Se selittää myös heidän vastavuoroisuutensa. Aihe kattaa myös trigonometristen kulmien, erityisesti 30-, 45-ja 60-asteen erikoiskulmien, arvioinnin.

oppaassa käsitellään lopuksi trigonometristen funktioiden käänteislukuja ja kahta yleisintä tapaa mitata kulmia.

• tunnista oikeiden kolmioiden sivut
• trigonometriset funktiot eli Trig. Suhteet
• Sini
• kosini

tangentti

• katsaus Siniin, kosiniin ja tangenttiin
• Sekantti, Kosekantti, kotangentti
• Sin, Cos, Tan, Sec, Csc, cotangentti
• Yhteisfunktiot
• arvioivat trigonometriset kulmat
• Erikoiskulmat: 30-asteista, 45-asteista, 60-asteista
• käyttäen laskinta
• käänteistä trigonometriaa
• asteita ja radiaaneja

trigonometrian sovelluksia

trigonometrisille funktioille on itse asiassa monenlaisia teoreettisia ja käytännöllisiä sovelluksia. Niiden avulla voidaan löytää kolmiosta puuttuvat sivut tai kulmat, mutta niiden avulla voidaan myös selvittää sillan tukipalkkien pituus tai varjon perusteella korkean kohteen korkeus.

tämä aihepiiri käsittelee erityyppisiä trigonometrian ongelmia ja sitä, miten trigonometristen perusfunktioiden avulla voidaan löytää tuntemattomia sivupituuksia. Se kattaa myös sen, miten niitä voidaan käyttää kulmien löytämiseen ja jopa kolmion pinta-alaan.

Tämä jakso päättyy Alatopioihin Sinesin laeista ja kosinien laeista.

• trigonometrian ongelmat
• Siniongelmat
• Kosiniongelmat
• Tangenttiongelmat
• Etsi objektin korkeus trigonometrian avulla
• trigonometrian Sovellukset
• korkeus-ja Painokulma
• kolmion alue Sinifunktion avulla
• Sinin tai Sinin säännön
• kosinilaki tai Kosinisääntö

Trigonometria Karteesisessa tasossa

Trigonometria karteesisessa tasossa keskittyy yksikköympyrän ympärille. Toisin sanoen ympyrän keskipisteessä pisteessä (0, 0), jonka säde on 1. Mikä tahansa suora, joka yhdistää Origon ympyrän pisteeseen, voidaan konstruoida suorakulmaiseksi kolmioksi, jonka hypotenuusa on pituudeltaan 1. Kolmion jalkojen pituudet antavat käsityksen trigonometrisistä funktioista. Yksikköympyrän syklisyys paljastaa myös kaavoitukseen käyttökelpoisten funktioiden kuviot.

tämä aihe alkaa kuvauksella kulmista vakioasennossa ja koterminaalikulmista ennen yksikköympyrän ja vertailukulmien selittämistä. Sen jälkeen se kattaa, miten trigonometristen funktioiden arvot muuttuvat karteesisen tason kvadrantin perusteella. Lopuksi tämä osio päättyy selittämällä, miten yksikköympyrää ja xy-tasoa voidaan käyttää trigonometrian ongelmien ratkaisemiseen.

• kulmat vakioasennossa ja Koterminaalikulmat
• Yksikköympyrä
• Referenssikulma
• löytää kvadrantti, jossa kulma sijaitsee
• trigonometriset funktiot Karteesisessa tasossa
• asteet ja Radiaanit
• arvioi trigonometriset funktiot kulmille, joille annetaan piste on the angle
• evaluating trigonometric functions using the reference Angle
• finding Trigonometric values given one Trigonometric value/other info
• evaluating Trigonometric Funktiot tärkeissä kulmissa

trigonometristen funktioiden kuvaajat

vaikka karteesisen tason yksikköympyrä tarjoaa trigonometrisiin funktioihin, jokaisella näistä funktioista on myös oma kuvaajansa. Nämä graafit ovat luonteeltaan syklisiä. Tyypillisesti trig-funktioiden kuvaajat ovat järkevimpiä, kun x-akseli jaetaan pi-radiaanien intervalleihin, kun taas y-akseli jaetaan vielä kokonaislukujen intervalleihin.

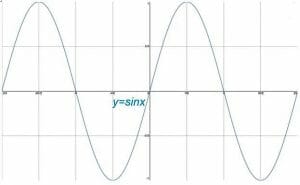
tämä aihealue kattaa sinin, kosinin ja tangentin peruskuviot. Sen jälkeen käsitellään muutoksia näiden kuvaajien ja niiden ominaisuuksia. Lopuksi aihe päättyy subtopic noin graafit, reciprocals, perus trig funktiot.

• trigonometrian kuvaajat
• Sinigrafiikka
• Kosinigrafiikka
• Tangenttigrafiikka
• trigonometristen kuvaajien muunnokset
• Sini – ja Kosinifunktioiden enimmäis-ja vähimmäisarvot
• Grafing Trig-funktiot: Amplitudi -, periodi -, pysty-ja vaakasuuntaiset siirtymät
• tangentti -, kotangentti -, Sekantti -, Kosekanttigrafiikat

trigonometriset identiteetit

Tämä on se kohta, jossa trigonometriset funktiot saavat oman elämän lukuun ottamatta niiden perustaa kolmion sivusuhteissa. Funktiot sisältävät lukuisia identiteettejä, jotka valaisevat erityyppisten trig-funktioiden välistä suhdetta.

näiden identiteettien avulla voidaan löytää yhteisten vertailukulmien ulkopuolisten kulmien arvot. Itse asiassa, ne olivat tärkein työkalu tehdä, että ennen laskimia.

tämä aihe selittää trigonometriset identiteetit ja niiden löytämisen ja muistamisen. Siinä selitetään myös, miten identiteettejä käytetään ilmaisujen yksinkertaistamiseen, johon liittyy melkoinen määrä algebrallista manipulaatiota.

oppaassa selitetään, miten eri kulmien arvot voidaan löytää vertailukulmien perusteella summa-ja erotusidentiteettien sekä kaksoiskulma-ja puolikulmiokaavojen avulla. Aihe jatkuu ja päättyy enemmän tapoja yksinkertaistaa, tekijä, ja ratkaista trigonometriset yhtälöt.

• trigonometriset identiteetit
• trigonometriset identiteetit: Miten johtaa/ muistaa ne
• käyttäen trigonometrisiä identiteettejä yksinkertaistamaan lausekkeita
• summa-ja Erotusidentiteettejä
• kaksois-ja Puolisulmakaavoja
• yksinkertaistaen trigonometrisiä lausekkeita käyttäen Trig-identiteettejä
• yksinkertaistaen trigonometrisiä lausekkeita käyttäen murtolukuja
• yksinkertaistaen binomien tuotteita, joihin liittyy trigonometrisiä funktioita
• faktorointi ja yksinkertaistaen trigonometrisiä lausekkeita
• ratkaisemalla Trigonometriset yhtälöt
• ratkaisemalla trigonometriset yhtälöt faktoroinnin avulla
• esimerkit jossa trigonometriset funktiot: parillinen, pariton tai kumpikaan
• todistaa trigonometrisen identiteetin