I triangoli possono sembrare semplici figure, ma la matematica dietro di loro è abbastanza profonda da essere considerata il suo soggetto: la trigonometria.

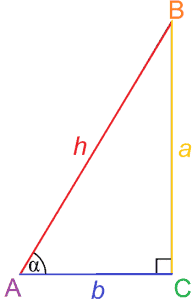
Come suggerisce il nome, la trigonometria è lo studio dei triangoli. Più specificamente, la trigonometria si occupa delle relazioni tra angoli e lati nei triangoli.

Un po ‘ sorprendentemente, i rapporti trigonometrici possono anche fornire una comprensione più ricca dei cerchi. Questi rapporti sono spesso usati nel calcolo e in molti rami della scienza, tra cui fisica, ingegneria e astronomia.

Le risorse in questa guida coprono le basi della trigonometria, inclusa una definizione di rapporti e funzioni trigonometriche. Poi vanno oltre come utilizzare queste funzioni nei problemi e come graficarli.

Infine, questa guida alle risorse si conclude con una spiegazione delle identità trigonometriche più comuni.

Trigonometria di base

La trigonometria si occupa in particolare dei rapporti dei lati in un triangolo rettangolo, che possono essere utilizzati per determinare la misura di un angolo. Questi rapporti sono chiamati funzioni trigonometriche e le più basilari sono seno e coseno.

Queste due funzioni sono utilizzate per definire le altre ben note funzioni trigonometriche: tangente, secante, cosecante e cotangente.

Questa sezione inizia esaminando i triangoli rettangoli e spiegando le funzioni trigonometriche di base. Spiega anche i loro reciproci. L’argomento copre anche come valutare gli angoli trigonometrici, in particolare gli angoli speciali di 30, 45 e 60 gradi.

Infine, la guida a questo argomento copre come affrontare gli inversi delle funzioni trigonometriche e i due modi più comuni per misurare gli angoli.

• Identificare i lati dei triangoli rettangoli
• Funzioni trigonometriche o Trigonometriche. Rapporti
• Seno
• Coseno
• Tangente
• Recensione di Seno, Coseno e Tangente
• Secante, Cosecante, Cotangente
• Sin, Cos, Tan, Sec, Csc, Culla
• Co-Funzioni
• Valutare Trigonometriche di Angoli
• Angoli Particolari: 30 Gradi, 45 gradi, 60 gradi
• Utilizzando una calcolatrice
• Trigonometria inversa
• Gradi e radianti

Applicazioni di trigonometria

Ci sono in realtà una vasta gamma di applicazioni teoriche e pratiche per le funzioni trigonometriche. Possono essere utilizzati per trovare lati o angoli mancanti in un triangolo, ma possono anche essere utilizzati per trovare la lunghezza delle travi di supporto per un ponte o l’altezza di un oggetto alto in base a un’ombra.

Questo argomento copre diversi tipi di problemi di trigonometria e come le funzioni trigonometriche di base possono essere utilizzate per trovare lunghezze laterali sconosciute. Copre anche il modo in cui possono essere utilizzati per trovare angoli e persino l’area di un triangolo.

Infine, questa sezione si conclude con argomenti secondari sulle Leggi dei seni e la Legge dei coseni.

• Trigonometria Problemi
• Sine Problemi
• Coseno Problemi
• Tangente Problemi
• Trovare Sconosciuto Lati dell’angolo retto
• Trovare l’Altezza di un Oggetto Utilizzando la Trigonometria
• Trigonometria Applicazioni
• Angolo di Elevazione e Depressione
• Area del Triangolo Utilizzando la Funzione Seno
• teorema dei seni o Sine Regola
• la Legge del Coseno o Coseno Regola

Trigonometria nel Piano Cartesiano

la Trigonometria nel Piano Cartesiano è centrata intorno al cerchio unitario. Cioè, il cerchio centrato nel punto (0, 0) con un raggio di 1. Qualsiasi linea che collega l’origine con un punto sul cerchio può essere costruita come un triangolo rettangolo con un’ipotenusa di lunghezza 1. Le lunghezze delle gambe del triangolo forniscono informazioni sulle funzioni trigonometriche. La natura ciclica del cerchio unitario rivela anche modelli nelle funzioni utili per la grafica.

Questo argomento inizia con una descrizione degli angoli nella posizione standard e negli angoli coterminali prima di spiegare il cerchio unitario e gli angoli di riferimento. Copre quindi come i valori delle funzioni trigonometriche cambiano in base al quadrante del piano cartesiano. Infine, questa sezione termina spiegando come il cerchio unitario e il piano xy possono essere utilizzati per risolvere i problemi di trigonometria.

• Angoli alla Posizione Standard e Coterminal Angoli
• Cerchio Unitario
• Angolo di Riferimento
• Rapporti Trigonometrici in Quattro Quadranti
• Trovare il Quadrante in Cui un Angolo si Trova
• Coterminal Angoli
• Funzioni Trigonometriche nel Piano Cartesiano
• Gradi e Radianti
• Valutare le Funzioni Trigonometriche per Angoli, Dato un Punto dell’Angolo
• la Valutazione di Funzioni Trigonometriche Utilizzando l’Angolo di Riferimento
• Trovare Trigonometriche i Valori di Una Trigonometriche Valore/Altre Info
• Valutare Trigonometriche Funzioni ad angoli importanti

Grafici delle funzioni trigonometriche

Sebbene il cerchio unitario nel piano cartesiano fornisca funzioni trigonometriche, ognuna di queste funzioni ha anche un proprio grafico. Questi grafici sono di natura ciclica. In genere, i grafici delle funzioni trigonometriche hanno più senso quando l’asse x è diviso in intervalli di radianti pi mentre l’asse y è ancora diviso in intervalli di numeri interi.

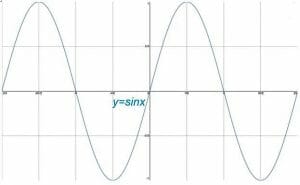
Questo argomento copre i grafici di base di seno, coseno e tangente. Quindi discute le trasformazioni di quei grafici e le loro proprietà. Infine, l’argomento si conclude con un argomento secondario sui grafici dei reciproci delle funzioni trigonometriche di base.

• Trigonometria Grafici
• Sine Grafico
• Coseno Grafico
• Tangente il Grafico
• Trasformazioni di Trigonometriche Grafici
• Grafica Seno e Coseno con Coefficienti Diversi
• i Valori Massimi e Minimi delle Funzioni Seno e Coseno
• Grafica Funzioni Trigonometriche: Ampiezza, Periodo, Spostamenti verticali e orizzontali
• Grafici tangenti, cotangenti, secanti, Cosecanti

Identità trigonometriche

Questo è il punto in cui le funzioni trigonometriche assumono una vita propria a parte la loro base nei rapporti lato triangolo. Le funzioni contengono numerose identità che illuminano la relazione tra diversi tipi di funzioni trigonometriche.

Queste identità possono essere utilizzate per trovare i valori degli angoli al di fuori degli angoli di riferimento comuni. In realtà, erano lo strumento principale disponibile per farlo prima delle calcolatrici.

Questo argomento spiega le identità trigonometriche e come trovarle e ricordarle. Spiega anche come utilizzare le identità per semplificare le espressioni, il che comporta una buona dose di manipolazione algebrica.

La guida continua a spiegare come trovare i valori di angoli diversi in base agli angoli di riferimento con le identità somma e differenza e le formule doppio angolo e mezzo angolo. L’argomento continua e si conclude con altri modi per semplificare, fattore, e risolvere equazioni trigonometriche.

• Identità trigonometriche
• Identità trigonometriche: Come Ricavare/ Li Ricordo
• Utilizza le Identità Trigonometriche per Semplificare Espressioni
• la Somma e la Differenza di Identità
• Doppio-Angolo e Mezza-le Formule di Angolo
• le Equazioni Trigonometriche
• Semplificare le Espressioni Trigonometriche Utilizzando Trig Identità
• la Semplificazione Trigonometriche Espressioni con le Frazioni
• la Semplificazione Prodotti di Binomi che Coinvolgono le Funzioni Trigonometriche
• Di Factoring e di Semplificare le Espressioni Trigonometriche
• Risoluzione di Equazioni Trigonometriche
• Risoluzione di Equazioni Trigonometriche Utilizzo di Factoring
• Esempi con funzioni trigonometriche: Pari, dispari o nessuna delle due
• Dimostrando un’identità trigonometrica