triunghiurile pot părea simple figuri, dar matematica din spatele lor este suficient de adâncă pentru a fi considerată propriul subiect: trigonometria.

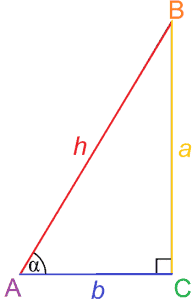
după cum sugerează și numele, trigonometria este studiul triunghiurilor. Mai precis, trigonometria se ocupă de relațiile dintre unghiuri și laturi în triunghiuri.oarecum surprinzător, raporturile trigonometrice pot oferi, de asemenea, o înțelegere mai bogată a cercurilor. Aceste rapoarte sunt adesea folosite în calcul, precum și în multe ramuri ale științei, inclusiv fizica, ingineria și astronomia.

resursele din acest ghid acoperă elementele de bază ale trigonometriei, inclusiv o definiție a raporturilor și funcțiilor trigonometrice. Apoi trec peste modul de utilizare a acestor funcții în probleme și cum să le graficăm.

în cele din urmă, acest ghid de resurse se încheie cu o explicație a celor mai comune Identități trigonometrice.

trigonometria de bază

trigonometria se ocupă în special de raporturile laturilor într-un triunghi dreptunghiular, care poate fi utilizat pentru a determina măsura unui unghi. Aceste rapoarte se numesc funcții trigonometrice, iar cele mai de bază sunt sinusul și cosinusul.

aceste două funcții sunt folosite pentru a defini celelalte funcții trigonometrice bine cunoscute: tangentă, secantă, cosecantă și cotangentă.

această secțiune începe prin revizuirea triunghiurilor dreptunghiulare și explicarea funcțiilor trigonometrice de bază. De asemenea, explică reciprocitățile lor. Subiectul acoperă, de asemenea, modul de evaluare a unghiurilor trigonometrice, în special unghiurile speciale de 30, 45 și 60 de grade.

în cele din urmă, ghidul acestui subiect acoperă modul de abordare a inverselor funcțiilor trigonometrice și a celor mai comune două moduri de măsurare a unghiurilor.

• identificați laturile triunghiurilor drepte
• Funcții trigonometrice sau trigonometrice. Raporturi
• sinus
• cosinus
• tangentă
• revizuirea sinusului, cosinusului și tangentei
• Secant, Cosecant, Cotangent
• păcat, Cos, bronz, Sec, Csc, Cot
• Co-funcții
• evaluează unghiurile trigonometrice
• Unghiuri speciale: 30 de grade, 45 de grade, 60 de Grade
• folosind un Calculator
• Trigonometrie inversă
• grade și radiani

aplicații ale trigonometriei

există de fapt o mare varietate de aplicații teoretice și practice pentru funcțiile trigonometrice. Ele pot fi folosite pentru a găsi laturile sau unghiurile lipsă într-un triunghi, dar pot fi folosite și pentru a găsi lungimea grinzilor de susținere pentru un pod sau înălțimea unui obiect înalt bazat pe o umbră.

acest subiect acoperă diferite tipuri de probleme de trigonometrie și modul în care funcțiile trigonometrice de bază pot fi utilizate pentru a găsi lungimi laterale necunoscute. De asemenea, acoperă modul în care pot fi folosite pentru a găsi unghiuri și chiar aria unui triunghi.

în cele din urmă, această secțiune se încheie cu subteme despre legile sinelor și Legea Cosinusurilor.

• probleme de Trigonometrie
• probleme de sinus
• probleme de cosinus
• probleme tangente
• găsiți laturile necunoscute ale unghiurilor drepte
• găsiți înălțimea obiectului folosind trigonometria
• aplicații de Trigonometrie
• unghiul de elevație și depresie
• zona triunghiului folosind funcția sinusoidală
• Legea sinusului sau regula sinusoidală
• /li>
• legea cosinusului sau regula cosinusului

trigonometria în planul cartezian

trigonometria în planul cartezian este centrată în jurul cercului unității. Adică cercul centrat în punctul (0, 0) cu o rază de 1. Orice linie care leagă originea cu un punct de pe cerc poate fi construită ca un triunghi dreptunghiular cu o ipotenuză de lungime 1. Lungimile picioarelor triunghiului oferă o perspectivă asupra funcțiilor trigonometrice. Natura ciclică a cercului unității dezvăluie, de asemenea, modele în funcțiile care sunt utile pentru grafică.

acest subiect începe cu o descriere a unghiurilor la poziția standard și unghiurile coterminale înainte de a explica cercul unității și unghiurile de referință. Apoi acoperă modul în care valorile funcțiilor trigonometrice se schimbă pe baza cadranului planului cartezian. În cele din urmă, această secțiune se încheie explicând modul în care cercul unității și planul xy pot fi utilizate pentru a rezolva problemele de trigonometrie.

• unghiuri la poziția Standard și unghiuri Coterminale
• cerc unitar
• unghi de referință
• raporturi trigonometrice în cele patru cadrane
• găsirea cadranului în care se află un unghi
• unghiuri Coterminale
• Funcții trigonometrice în planul cartezian
• grade și radiani
• evaluarea funcțiilor trigonometrice pentru un unghi, având în vedere un punct pe unghiul
• evaluarea funcțiilor trigonometrice folosind unghiul de referință
• găsirea valorilor trigonometrice date o valoare trigonometrică/alte informații
• evaluarea trigonometrică Funcții la unghiuri importante

grafice ale funcțiilor trigonometrice

deși cercul unitate în planul cartezian prevede în funcții trigonometrice, fiecare dintre aceste funcții are, de asemenea, propriul grafic. Aceste grafice sunt ciclice în natură. De obicei, graficele funcțiilor trigonometrice au cel mai mult sens atunci când axa x este împărțită în intervale de radiani pi, în timp ce axa y este încă împărțită în intervale de numere întregi.

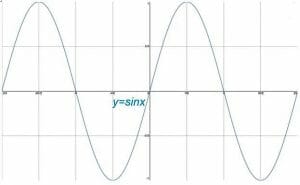
acest subiect acoperă graficele de bază ale sinusului, cosinusului și tangentei. Apoi discută transformările acestor grafice și proprietățile lor. În cele din urmă, subiectul se încheie cu un subtopic despre graficele reciprocelor funcțiilor trig de bază.

• grafice trigonometrice
• Grafic sinus
• Grafic cosinus
• Grafic Tangent
• transformări ale graficelor trigonometrice
• Grafic sinus și cosinus cu coeficienți diferiți
• valori maxime și minime ale funcțiilor sinus și cosinus
• Grafic funcții Trig: Amplitudine, perioadă, schimbări verticale și orizontale
• grafice tangente, cotangente, secante, cosecante

Identități trigonometrice

acesta este punctul în care funcțiile trigonometrice își iau o viață proprie în afară de baza lor în raporturi laterale triunghiulare. Funcțiile conțin numeroase identități care luminează relația dintre diferite tipuri de funcții trigonometrice.

aceste identități pot fi folosite pentru a găsi valorile unghiurilor în afara unghiurilor de referință comune. De fapt, acestea au fost principalul instrument disponibil pentru a face acest lucru înainte de calculatoare.

acest subiect explică identitățile trigonometrice și cum să le găsiți și să le amintiți. De asemenea, explică modul de utilizare a identităților pentru a simplifica expresiile, ceea ce implică o cantitate echitabilă de manipulare algebrică.

ghidul continuă să explice cum să găsiți valorile diferitelor unghiuri pe baza unghiurilor de referință cu identitățile sumă și diferență și formulele cu unghi dublu și jumătate de unghi. Subiectul continuă și se încheie cu mai multe modalități de simplificare, factor și rezolvare a ecuațiilor trigonometrice.

• Identități trigonometrice
• Identități trigonometrice: Cum de a deriva/ amintiți-le
• folosind Identități trigonometrice pentru a simplifica expresii
• suma și diferența identități
• formule dublu-unghi și jumătate unghi
• ecuații trigonometrice
• simplificarea expresii trigonometrice folosind identități Trig
• simplificarea expresii trigonometrice care implică fracții
• simplificarea produselor binomiale care implică funcții trigonometrice
• Factoring și simplificarea expresii trigonometrice
• rezolvarea ecuațiilor trigonometrice
• rezolvarea ecuațiilor trigonometrice folosind factoring
• exemple cu funcții trigonometrice: Par, impar sau niciunul
• dovedind o identitate trigonometrică