driehoeken lijken misschien eenvoudige figuren, maar de wiskunde erachter is diep genoeg om als zijn eigen onderwerp te worden beschouwd: trigonometrie.

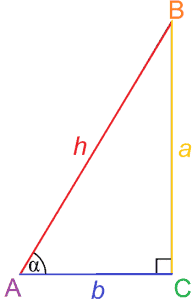
zoals de naam al doet vermoeden, is trigonometrie de studie van driehoeken. Meer specifiek gaat trigonometrie over de relaties tussen hoeken en zijden in driehoeken.

enigszins verrassend kunnen de trigonometrische verhoudingen ook een beter begrip van cirkels geven. Deze verhoudingen worden vaak gebruikt in calculus evenals vele takken van wetenschap met inbegrip van natuurkunde, techniek, en astronomie.

de bronnen in deze gids hebben betrekking op de basisbeginselen van de trigonometrie, met inbegrip van een definitie van trigonometrische ratio ‘ s en functies. Ze gaan dan over hoe deze functies te gebruiken in problemen en hoe ze grafisch te maken.

ten slotte wordt deze resource guide afgesloten met een uitleg van de meest voorkomende trigonometrische identiteiten.

Basic Trigonometry

Trigonometrie behandelt in het bijzonder de verhoudingen van zijden in een rechthoekige driehoek, die kunnen worden gebruikt om de maat van een hoek te bepalen. Deze verhoudingen worden trigonometrische functies genoemd, en de meest fundamentele zijn sinus en cosinus.

deze twee functies worden gebruikt om de andere bekende trigonometrische functies te definiëren: tangent, secant, cosecant en cotangent.

Deze sectie begint met het bekijken van rechthoekige driehoeken en het uitleggen van de fundamentele trigonometrische functies. Het verklaart ook hun wederkerigheid. Het onderwerp behandelt ook hoe trigonometrische hoeken te evalueren, met name de speciale hoeken van 30-, 45-en 60-graden.

ten slotte behandelt De Gids Voor dit onderwerp Hoe om te gaan met de inverse van trigonometrische functies en de twee meest voorkomende manieren om hoeken te meten.

• Identificeer de zijden van rechthoekige driehoeken
• trigonometrische functies of Trig. Ratio ‘ s
• sinus
• cosinus
• raaklijn
• overzicht van sinus, cosinus en tangens
• Secant, Cosecant, Cotangent
• Sin, Cos, Tan, Sec, CSC, Cot
• Co-functies
• trigonometrische hoeken
• evaluatie van trigonometrische hoeken
• speciale hoeken: 30-graden, 45-graden, 60-graden
• met behulp van een Calculator
• Inverse Trigonometrie
• graden en radialen

toepassingen van Trigonometrie

Er zijn eigenlijk een grote verscheidenheid aan theoretische en praktische toepassingen voor trigonometrische functies. Ze kunnen worden gebruikt om ontbrekende zijden of hoeken in een driehoek te vinden, maar ze kunnen ook worden gebruikt om de lengte van steunbalken voor een brug of de hoogte van een hoog object op basis van een schaduw te vinden.

dit onderwerp behandelt verschillende soorten trigonometrieproblemen en hoe de basis trigonometrische functies kunnen worden gebruikt om onbekende zijlengtes te vinden. Het behandelt ook hoe ze kunnen worden gebruikt om hoeken en zelfs de oppervlakte van een driehoek te vinden.

ten slotte wordt deze sectie afgesloten met subonderwerpen over de wetten van Sines en de wet van Cosines.

• Trigonometrieproblemen
• sinusproblemen
• cosinus problemen
• raakvlakken
• vind Onbekende zijden van rechte hoeken
• vind hoogte van Object met behulp van Trigonometrie
• Trigonometrietoepassingen
• hoek van hoogte en depressie
• oppervlakte van driehoek met behulp van de sinusfunctie
• wet van sinussen of sinusregel
• de cosinusregel

trigonometrie in het cartesiaanse vlak

trigonometrie in het Cartesiaanse vlak is gecentreerd rond de eenheidscirkel. Dat wil zeggen, de cirkel gecentreerd op het punt (0, 0) met een straal van 1. Elke lijn die de oorsprong verbindt met een punt op de cirkel kan worden geconstrueerd als een rechthoekige driehoek met een schuine zijde van lengte 1. De lengtes van de poten van de driehoek geven inzicht in de trigonometrische functies. De cyclische aard van de eenheidscirkel onthult ook patronen in de functies die nuttig zijn voor het grafisch maken.

dit onderwerp begint met een beschrijving van hoeken op de standaardpositie en coterminale hoeken alvorens de eenheidscirkel en referentiehoeken uit te leggen. Het behandelt dan hoe de waarden van de trigonometrische functies veranderen gebaseerd op het kwadrant van het Cartesiaanse vlak. Tot slot wordt in deze sectie uitgelegd hoe de eenheidscirkel en het xy-vlak kunnen worden gebruikt om trigonometrieproblemen op te lossen.

• Hoeken op de Standaard Positie en Coterminal Hoeken
• eenheidscirkel
• Referentie Hoek
• Goniometrische Verhoudingen in de Vier Kwadranten
• het Vinden van het Kwadrant Waarin een Hoek Ligt
• Coterminal Hoeken
• Goniometrische Functies in het Cartesisch Vlak
• Graden en Radialen
• het Evalueren van Goniometrische Functies voor een Hoek, Gegeven een Punt op de Hoek
• Evaluatie van Goniometrische Functies met Behulp van de Referentie Hoek
• het Vinden van Goniometrische Waarden Gegeven Een Goniometrische Waarde/Andere Info
• Evaluatie van Trigonometrische Functies onder belangrijke hoeken

grafieken van trigonometrische functies

hoewel de eenheidscirkel in het Cartesiaanse vlak voorziet in trigonometrische functies, heeft elk van deze functies ook zijn eigen grafiek. Deze grafieken zijn cyclisch van aard. Typisch, grafieken van trig functies maken het meest zinvol wanneer de x-as is verdeeld in intervallen van pi radialen terwijl de y-as is nog steeds verdeeld in intervallen van hele getallen.

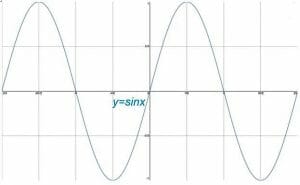
dit onderwerp behandelt de basisgrafieken van sinus, cosinus en tangens. Het bespreekt dan transformaties van die grafieken en hun eigenschappen. Tot slot, het onderwerp eindigt met een subtopisch over de grafieken van de reciproken van de fundamentele trig functies.

• Trigonometriegrafieken
• Sinusgrafiek
• Cosinusgrafiek
• Raakgrafiek
• transformaties van trigonometrische grafieken
• grafieken sinus en cosinus met verschillende coëfficiënten
• Maximum-en minimumwaarden van sinus-en Cosinusfuncties
• grafieken Trigfuncties: Amplitude, periode, Verticale En Horizontale verschuivingen
• Rangent, Cotangent, Secant, Cosecant grafieken

trigonometrische identiteiten

Dit is het punt waar trigonometrische functies een eigen levensduur hebben, afgezien van hun basis in driehoekige zijverhoudingen. De functies bevatten talrijke identiteiten die de relatie tussen verschillende soorten trig-functies verlichten.

deze identiteiten kunnen worden gebruikt om de waarden van hoeken buiten de gemeenschappelijke referentiehoeken te vinden. In feite, ze waren de belangrijkste tool beschikbaar om dat te doen voor rekenmachines.

dit onderwerp legt trigonometrische identiteiten uit en hoe ze te vinden en te onthouden. Het legt ook uit hoe de identiteiten te gebruiken om uitdrukkingen te vereenvoudigen, wat een behoorlijke hoeveelheid algebraïsche manipulatie impliceert.

De Gids legt verder uit hoe de waarden van verschillende hoeken kunnen worden gevonden op basis van referentiehoeken met de som-en verschilidentiteiten en de formules met dubbele en halve hoek. Het onderwerp gaat verder en eindigt met meer manieren om trigonometrische vergelijkingen te vereenvoudigen, te factureren en op te lossen.

• trigonometrische identiteiten
• trigonometrische identiteiten: Hoe ze af te leiden/ te onthouden
• met behulp van trigonometrische identiteiten om expressies te vereenvoudigen
• som-en Verschilidentiteiten
• formules met dubbele en halve hoek
• trigonometrische vergelijkingen
• simplifying trigonometrische expressies met behulp van trigonometrische identiteiten
• Simplifying trigonometrische expressies met fracties
• Simplifying Products of Binomials with trigonometrische functies
• Factoring and Simplifying trigonometrische uitdrukkingen
• oplossen van trigonometrische vergelijkingen
• oplossen van trigonometrische vergelijkingen met factoring
• voorbeelden met trigonometrische functies: Even, oneven of geen
• waaruit een trigonometrische identiteit blijkt