Triangler kan virke som enkle figurer, men matematikken bag dem er dyb nok til at blive betragtet som sit eget emne: trigonometri.

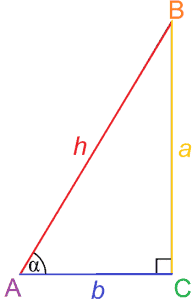
Som navnet antyder, er trigonometri studiet af trekanter. Mere specifikt omhandler trigonometri forholdet mellem vinkler og sider i trekanter.

noget overraskende kan de trigonometriske forhold også give en rigere forståelse af cirkler. Disse forhold bruges ofte i beregning såvel som mange grene af videnskab, herunder fysik, ingeniørarbejde og astronomi.

ressourcerne i denne vejledning dækker det grundlæggende i trigonometri, herunder en definition af trigonometriske forhold og funktioner. De går derefter over, hvordan man bruger disse funktioner i problemer, og hvordan man tegner dem.

endelig afsluttes denne ressourcevejledning med en forklaring på de mest almindelige trigonometriske identiteter.

grundlæggende trigonometri

Trigonometri omhandler især forholdet mellem sider i en højre trekant, som kan bruges til at bestemme målingen af en vinkel. Disse forhold kaldes trigonometriske funktioner, og de mest basale er sinus og cosinus.

disse to funktioner bruges til at definere de andre velkendte trigonometriske funktioner: tangent, secant, cosecant og cotangent.

dette afsnit begynder med at gennemgå højre trekanter og forklare de grundlæggende trigonometriske funktioner. Det forklarer også deres gensidige. Emnet dækker også, hvordan man vurderer trigonometriske vinkler, især de specielle vinkler på 30 -, 45-og 60-grader.

endelig dækker vejledningen til dette emne, hvordan man håndterer inverserne af trigonometriske funktioner og de to mest almindelige måder at måle vinkler på.

• Identificer siderne af højre trekanter
• trigonometriske funktioner eller Trig. Forhold
• sinus
• cosinus
• Tangent
• gennemgang af sinus, cosinus og Tangent
• Secant, cosecant, Cotangent
• Sin, Cos, Tan, Sec, Csc, Cot
• Co-funktioner
• Evaluer trigonometriske vinkler
• særlige vinkler: 30 grader, 45 grader, 60 grader
• brug af en lommeregner
• invers Trigonometri
• grader og radianer

anvendelser af Trigonometri

der er faktisk en lang række teoretiske og praktiske anvendelser til trigonometriske funktioner. De kan bruges til at finde manglende sider eller vinkler i en trekant, men de kan også bruges til at finde længden af støttebjælker til en bro eller højden på en høj genstand baseret på en skygge.

dette emne dækker forskellige typer trigonometriproblemer, og hvordan de grundlæggende trigonometriske funktioner kan bruges til at finde ukendte sidelængder. Det dækker også, hvordan de kan bruges til at finde vinkler og endda arealet af en trekant.

endelig afsluttes dette afsnit med underemner om Sines love og Cosines lov.

• Trigonometri problemer
• Sine problemer
• cosinus problemer
• Tangent problemer
• Find ukendte sider af rette vinkler
• Find objektets højde ved hjælp af Trigonometri
• Trigonometri applikationer
• vinkel på højde og Depression
• område af trekant ved hjælp af sinusfunktionen
• lov om Sines eller Sinusregel
• lov om cosinus eller cosinus regel

trigonometri i det kartesiske plan

trigonometri i det kartesiske plan er centreret omkring enhedscirklen. Det vil sige cirklen centreret ved punktet (0, 0) med en radius på 1. Enhver linje, der forbinder oprindelsen med et punkt på cirklen, kan konstrueres som en højre trekant med en hypotenuse af længde 1. Længderne af trekantens ben giver indsigt i de trigonometriske funktioner. Den cykliske karakter af enhedscirklen afslører også mønstre i de funktioner, der er nyttige til graftegning.

dette emne begynder med en beskrivelse af vinkler i standardpositionen og coterminalvinkler, før du forklarer enhedens cirkel og referencevinkler. Det dækker derefter, hvordan værdierne for de trigonometriske funktioner ændres baseret på kvadranten i det kartesiske plan. Endelig slutter dette afsnit med at forklare, hvordan enhedscirklen og Planet kan bruges til at løse trigonometriproblemer.

• vinkler ved standardposition og Coterminalvinkler
• enhedscirkel
• referencevinkel
• trigonometriske forhold i de fire kvadranter
• find den kvadrant, hvor en vinkel ligger
• Coterminalvinkler
• trigonometriske funktioner i det kartesiske plan
• grader og radianer
• evaluering af trigonometriske funktioner for en vinkel, givet en punkt på vinklen
• evaluering af trigonometriske funktioner ved hjælp af referencevinklen
• find trigonometriske værdier givet en trigonometrisk værdi/anden info
• evaluering af trigonometrisk Funktioner i vigtige vinkler

grafer af trigonometriske funktioner

selvom enhedscirklen i det kartesiske plan tilvejebringer trigonometriske funktioner, har hver af disse funktioner også sin egen graf. Disse grafer er cykliske i naturen. Typisk giver grafer af trig-funktioner mest mening, når røntgenaksen er opdelt i intervaller af pi-radianer, mens y-aksen stadig er opdelt i intervaller af hele tal.

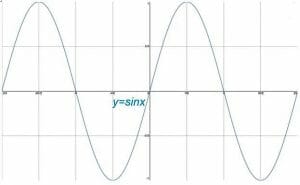
dette emne dækker de grundlæggende grafer af sinus, cosinus og tangent. Det diskuterer derefter transformationer af disse grafer og deres egenskaber. Endelig afsluttes emnet med et underemne om graferne for reciprokalerne for de grundlæggende trig-funktioner.

• Trigonometri grafer
• sinus Graph
• cosinus Graph
• Tangent Graph
• transformationer af trigonometriske grafer
• Graphing sinus og cosinus med forskellige koefficienter
• maksimum og Minimum værdier af sinus og cosinus funktioner
• Graphing Trig funktioner: Amplitude, periode, lodret og vandret Skift
• Tangent, Cotangent, Secant, Cosecant grafer

Trigonometriske identiteter

Dette er det punkt, hvor trigonometriske funktioner får deres eget liv bortset fra deres grundlag i trekantsideforhold. Funktionerne indeholder adskillige identiteter, der belyser forholdet mellem forskellige typer trig-funktioner.

disse identiteter kan bruges til at finde værdierne for vinkler uden for de fælles referencevinkler. Faktisk var de det vigtigste værktøj til rådighed for at gøre det før regnemaskiner.

dette emne forklarer trigonometriske identiteter og hvordan man finder og husker dem. Det forklarer også, hvordan man bruger identiteterne til at forenkle udtryk, hvilket indebærer en hel del algebraisk manipulation.

vejledningen fortsætter med at forklare, hvordan man finder værdierne for forskellige vinkler baseret på referencevinkler med sum-og forskelidentiteterne og formlerne med dobbeltvinkel og halvvinkel. Emnet fortsætter og afsluttes med flere måder at forenkle, faktorere og løse trigonometriske ligninger på.

• Trigonometriske identiteter
• Trigonometriske identiteter: Sådan udledes/ husker du dem
• brug af trigonometriske identiteter til at forenkle udtryk
• Sum og forskel identiteter
• Dobbeltvinkel-og Halvvinkelformler
• Trigonometriske ligninger
• forenkling af trigonometriske udtryk ved hjælp af Trig-identiteter
• forenkling af trigonometriske udtryk, der involverer fraktioner
• forenkling af produkter af Binomier, der involverer trigonometriske funktioner
• Factoring og forenkling af trigonometriske udtryk
• forenkling af trigonometriske udtryk, der involverer fraktioner
• forenkling af produkter af Binomier, der involverer trigonometriske funktioner
• Factoring og forenkling af trigonometriske udtryk
• løsning af trigonometriske ligninger
• løsning af trigonometriske ligninger ved hjælp af factoring
• eksempler med trigonometriske funktioner: lige, ulige eller ingen
• bevis for en trigonometrisk identitet