Dreiecke mögen wie einfache Figuren erscheinen, aber die Mathematik dahinter ist tief genug, um als ein eigenes Thema betrachtet zu werden: Trigonometrie.

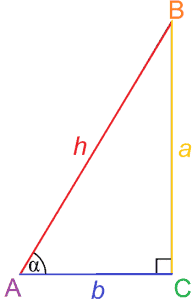
Wie der Name schon sagt, ist Trigonometrie das Studium von Dreiecken. Genauer, Trigonometrie befasst sich mit den Beziehungen zwischen Winkeln und Seiten in Dreiecken.Überraschenderweise können die trigonometrischen Verhältnisse auch ein besseres Verständnis von Kreisen vermitteln. Diese Verhältnisse werden häufig in der Infinitesimalrechnung sowie in vielen Wissenschaftszweigen wie Physik, Ingenieurwesen und Astronomie verwendet.

Die Ressourcen in diesem Handbuch behandeln die Grundlagen der Trigonometrie, einschließlich einer Definition von trigonometrischen Verhältnissen und Funktionen. Sie gehen dann darüber, wie man diese Funktionen in Problemen verwendet und wie man sie grafisch darstellt.

Schließlich schließt dieser Ressourcenleitfaden mit einer Erklärung der häufigsten trigonometrischen Identitäten.

Grundlegende Trigonometrie

Die Trigonometrie befasst sich insbesondere mit den Seitenverhältnissen in einem rechtwinkligen Dreieck, mit denen das Maß eines Winkels bestimmt werden kann. Diese Verhältnisse werden trigonometrische Funktionen genannt, und die grundlegendsten sind Sinus und Cosinus.

Diese beiden Funktionen werden verwendet, um die anderen bekannten trigonometrischen Funktionen zu definieren: Tangens, secant, cosecant und cotangent.

In diesem Abschnitt werden zunächst rechtwinklige Dreiecke überprüft und die grundlegenden trigonometrischen Funktionen erläutert. Es erklärt auch ihre Gegenseitigkeit. Das Thema behandelt auch die Bewertung trigonometrischer Winkel, insbesondere der speziellen Winkel von 30-, 45- und 60-Grad.

Schließlich behandelt der Leitfaden zu diesem Thema den Umgang mit den Inversen trigonometrischer Funktionen und die beiden gebräuchlichsten Methoden zum Messen von Winkeln.

• Identifizieren Sie die Seiten von rechtwinkligen Dreiecken
• Trigonometrische Funktionen oder Trig. Sinus
• Cosinus
• Tangens
• Überprüfung von Sinus, Cosinus und Tangens
• Sekante, Kosekante, Kotangens
• Sin, Cos, Tan, Sec, Csc, Cot
• Kofunktionen
• Trigonometrische Winkel auswerten
• Spezielle Winkel: 30-Grad, 45-Grad, 60-Grad
• Mit einem Taschenrechner
• Inverse Trigonometrie
• Grad und Bogenmaß

Anwendungen der Trigonometrie

Es gibt tatsächlich eine Vielzahl von theoretischen und praktischen Anwendungen für trigonometrische Funktionen. Sie können verwendet werden, um fehlende Seiten oder Winkel in einem Dreieck zu finden, aber sie können auch verwendet werden, um die Länge von Stützbalken für eine Brücke oder die Höhe eines hohen Objekts basierend auf einem Schatten zu finden.

Dieses Thema behandelt verschiedene Arten von trigonometrischen Problemen und wie die grundlegenden trigonometrischen Funktionen verwendet werden können, um unbekannte Seitenlängen zu finden. Es behandelt auch, wie sie verwendet werden können, um Winkel und sogar die Fläche eines Dreiecks zu finden.

Schließlich schließt dieser Abschnitt mit Unterthemen zu den Sinusgesetzen und dem Kosinusgesetz.

• Trigonometrieprobleme
• Sinusprobleme
• Cosinusprobleme
• Tangentenprobleme
• Unbekannte Seiten rechter Winkel finden
• Höhe des Objekts mithilfe der Trigonometrie ermitteln
• Trigonometrieanwendungen
• Höhen- und Senkungswinkel
• Fläche des Dreiecks mit der Sinusfunktion
• Sinusgesetz oder Sinusregel
• Kosinusgesetz oder Kosinusregel

Trigonometrie in der kartesischen Ebene

Die Trigonometrie in der kartesischen Ebene ist um den Einheitskreis zentriert. Das heißt, der Kreis zentriert auf den Punkt (0, 0) mit einem Radius von 1. Jede Linie, die den Ursprung mit einem Punkt auf dem Kreis verbindet, kann als rechtwinkliges Dreieck mit einer Hypotenuse der Länge 1 konstruiert werden. Die Längen der Schenkel des Dreiecks geben Einblick in die trigonometrischen Funktionen. Die zyklische Natur des Einheitskreises zeigt auch Muster in den Funktionen, die für die grafische Darstellung nützlich sind.

Dieses Thema beginnt mit einer Beschreibung der Winkel an der Standardposition und der Coterminalwinkel, bevor der Einheitskreis und die Referenzwinkel erläutert werden. Anschließend wird behandelt, wie sich die Werte der trigonometrischen Funktionen basierend auf dem Quadranten der kartesischen Ebene ändern. Abschließend wird in diesem Abschnitt erläutert, wie der Einheitskreis und die xy-Ebene zur Lösung von Trigonometrieproblemen verwendet werden können.

• Winkel an Standardposition und Koterminalwinkel
• Einheitskreis
• Referenzwinkel
• Trigonometrische Verhältnisse in den vier Quadranten
• Den Quadranten finden, in dem ein Winkel liegt
• Koterminalwinkel
• Trigonometrische Funktionen in der kartesischen Ebene
• Grad und Bogenmaß
• Trigonometrische Funktionen für einen Winkel bei gegebenem Punkt auswerten über den Winkel
• Trigonometrische Funktionen unter Verwendung des Referenzwinkels auswerten
• Trigonometrische Werte finden Bei einem trigonometrischen Wert / Andere Informationen
• Trigonometrische Funktionen auswerten Funktionen in wichtigen Winkeln

Graphen trigonometrischer Funktionen

Obwohl der Einheitskreis in der kartesischen Ebene in trigonometrische Funktionen unterteilt ist, hat jede dieser Funktionen auch einen eigenen Graphen. Diese Graphen sind zyklischer Natur. Typischerweise sind Graphen von Triggerfunktionen am sinnvollsten, wenn die x-Achse in Intervalle von Pi-Bogenmaß unterteilt ist, während die y-Achse immer noch in Intervalle von ganzen Zahlen unterteilt ist.

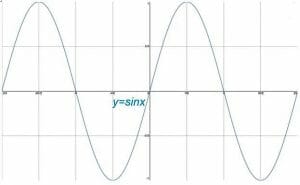
Dieses Thema behandelt die grundlegenden Graphen von Sinus, Cosinus und Tangens. Anschließend werden Transformationen dieser Graphen und ihrer Eigenschaften erörtert. Schließlich schließt das Thema mit einem Unterthema über die Graphen der Kehrwerte der grundlegenden Triggerfunktionen.

• Trigonometrische Graphen
• Sinusgraph
• Cosinusgraph
• Tangentgraph
• Transformationen von trigonometrischen Graphen
• Darstellung von Sinus und Cosinus mit unterschiedlichen Koeffizienten
• Maximal- und Minimalwerte von Sinus- und Cosinusfunktionen
• Darstellung von Triggerfunktionen: Amplitude, Periode, vertikale und horizontale Verschiebungen
• Tangens-, Kotangens-, Sekanten-, Kosekantengraphen

Trigonometrische Identitäten

Dies ist der Punkt, an dem trigonometrische Funktionen ein Eigenleben annehmen, abgesehen von ihrer Basis in Dreiecksseitenverhältnissen. Die Funktionen enthalten zahlreiche Identitäten, die die Beziehung zwischen verschiedenen Arten von Triggerfunktionen beleuchten.

Diese Identitäten können verwendet werden, um die Werte von Winkeln außerhalb der gemeinsamen Referenzwinkel zu finden. Tatsächlich waren sie das Hauptwerkzeug, das dafür vor Taschenrechnern zur Verfügung stand.

Dieses Thema erklärt trigonometrische Identitäten und wie man sie findet und sich daran erinnert. Es wird auch erklärt, wie die Identitäten verwendet werden, um Ausdrücke zu vereinfachen, was eine angemessene Menge an algebraischer Manipulation beinhaltet.

In diesem Handbuch wird erläutert, wie die Werte verschiedener Winkel basierend auf Referenzwinkeln mit den Summen- und Differenzidentitäten sowie den Formeln für Doppelwinkel und Halbwinkel ermittelt werden. Das Thema wird fortgesetzt und schließt mit weiteren Möglichkeiten, trigonometrische Gleichungen zu vereinfachen, zu faktorisieren und zu lösen.

• Trigonometrische Identitäten
• Trigonometrische Identitäten: Wie man sie ableitet / sich daran erinnert
• Verwendung trigonometrischer Identitäten zur Vereinfachung von Ausdrücken
• Summen- und Differentialidentitäten
• Doppelwinkel- und Halbwinkelformeln
• Trigonometrische Gleichungen
• Vereinfachung trigonometrischer Ausdrücke mit trigonometrischen Identitäten
• Vereinfachung trigonometrischer Ausdrücke mit Brüchen
• Vereinfachung von Produkten von Binomen mit trigonometrischen Funktionen
• Factoring und Vereinfachung trigonometrischer Ausdrücke
• Lösen trigonometrischer Gleichungen
• Lösen trigonometrischer Gleichungen mit Factoring
• Beispiele mit trigonometrischen Funktionen: Gerade, ungerade oder Keine
• Nachweis einer trigonometrischen Identität