Los triángulos pueden parecer figuras simples, pero las matemáticas detrás de ellos son lo suficientemente profundas como para ser consideradas su propio tema: la trigonometría.

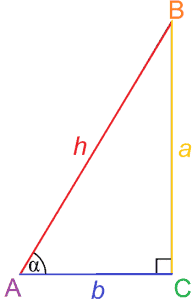
Como su nombre indica, la trigonometría es el estudio de triángulos. Más específicamente, la trigonometría se ocupa de las relaciones entre ángulos y lados en triángulos.

Sorprendentemente, las relaciones trigonométricas también pueden proporcionar una comprensión más rica de los círculos. Estas proporciones se utilizan a menudo en el cálculo, así como en muchas ramas de la ciencia, incluida la física, la ingeniería y la astronomía.

Los recursos de esta guía cubren los conceptos básicos de la trigonometría, incluida una definición de ratios y funciones trigonométricas. Luego repasan cómo usar estas funciones en problemas y cómo graficarlas.

Finalmente, esta guía de recursos concluye con una explicación de las identidades trigonométricas más comunes.

Trigonometría básica

La trigonometría se ocupa especialmente de las relaciones de lados en un triángulo rectángulo, que se puede usar para determinar la medida de un ángulo. Estas relaciones se llaman funciones trigonométricas, y las más básicas son seno y coseno.

Estas dos funciones se utilizan para definir las otras funciones trigonométricas conocidas: tangente, secante, cosecante y cotangente.

Esta sección comienza revisando los triángulos rectangulares y explicando las funciones trigonométricas básicas. También explica sus recíprocos. El tema también trata sobre cómo evaluar los ángulos trigonométricos, especialmente los ángulos especiales de 30, 45 y 60 grados.

Finalmente, la guía de este tema trata sobre cómo tratar los inversos de las funciones trigonométricas y las dos formas más comunes de medir ángulos.

• Identificar los Lados de los Triángulos rectángulos
• Funciones Trigonométricas o Trigonometría. Ratios
• Sine
• Coseno
• Tangente
• Examen de Seno, Coseno y Tangente
• Secante, Cosecante, la Cotangente
• sin, Cos, Tan, Sec, Csc, Cuna
• Co-Funciones
• Evaluar Trigonométricas de los Ángulos
• Especial Ángulos: 30 Grados, 45 Grados, 60 Grados
• Usando una calculadora
• Trigonometría inversa
• Grados y radianes

Aplicaciones de la trigonometría

En realidad hay una amplia variedad de aplicaciones teóricas y prácticas para funciones trigonométricas. Se pueden usar para encontrar lados o ángulos faltantes en un triángulo, pero también se pueden usar para encontrar la longitud de las vigas de soporte para un puente o la altura de un objeto alto basado en una sombra.

Este tema cubre diferentes tipos de problemas de trigonometría y cómo se pueden usar las funciones trigonométricas básicas para encontrar longitudes de lado desconocidas. También cubre cómo se pueden usar para encontrar ángulos e incluso el área de un triángulo.

Finalmente, esta sección concluye con subtemas sobre las Leyes de los Senos y la Ley de los Cosenos.

• Problemas de Trigonometría
• Problemas Sinusoidales
• Problemas de Coseno
• Problemas tangentes
• Encontrar Lados Desconocidos de Ángulos Rectos
• Encontrar la Altura del Objeto Mediante Trigonometría
• Aplicaciones de Trigonometría
• Ángulo de Elevación y Depresión
• Área del Triángulo Mediante la Función Seno
• Ley de Senos o Regla de Seno
• Ley de Cosenos o Regla de Coseno

La trigonometría en el Plano Cartesiano

La trigonometría en el Plano Cartesiano se centra alrededor del círculo unitario. Es decir, el círculo centrado en el punto (0, 0) con un radio de 1. Cualquier línea que conecte el origen con un punto en el círculo se puede construir como un triángulo rectángulo con una hipotenusa de longitud 1. Las longitudes de las patas del triángulo proporcionan una visión de las funciones trigonométricas. La naturaleza cíclica del círculo unitario también revela patrones en las funciones que son útiles para graficar.

Este tema comienza con una descripción de los ángulos en la posición estándar y los ángulos coterminales antes de explicar el círculo unitario y los ángulos de referencia. Luego cubre cómo cambian los valores de las funciones trigonométricas en función del cuadrante del Plano Cartesiano. Finalmente, esta sección termina explicando cómo el círculo unitario y el plano xy se pueden usar para resolver problemas de trigonometría.

• Ángulos en Posición Estándar y Ángulos Coterminales
• Círculo Unitario
• Ángulo de referencia
• Relaciones Trigonométricas en los Cuatro Cuadrantes
• Encontrar el Cuadrante en el que se Encuentra un Ángulo
• Ángulos Coterminales
• Funciones Trigonométricas en el Plano Cartesiano
• Grados y Radianes
• Evaluar Funciones Trigonométricas para un Ángulo, Dado un Punto en el Ángulo
• Evaluación de Funciones Trigonométricas Utilizando el Ángulo de Referencia
• Búsqueda de Valores Trigonométricos Dado Un Valor Trigonométrico/Otra Información
• Evaluación Trigonométrica Funciones en Ángulos Importantes

Gráficos de Funciones Trigonométricas

Aunque el círculo unitario en el plano cartesiano proporciona funciones trigonométricas, cada una de estas funciones también tiene su propio gráfico. Estos gráficos son de naturaleza cíclica. Típicamente, los gráficos de funciones trigonométricas tienen más sentido cuando el eje x se divide en intervalos de radianes pi, mientras que el eje y todavía se divide en intervalos de números enteros.

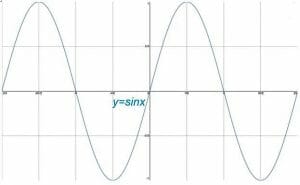
Este tema abarca los gráficos básicos de seno, coseno y tangente. Luego analiza las transformaciones de esos gráficos y sus propiedades. Finalmente, el tema concluye con un subtema sobre los gráficos de los recíprocos de las funciones trigonométricas básicas.

• Grafos de Trigonometría
• Grafo de Seno
• Grafo de Coseno
• Grafo Tangente
• Transformaciones de Grafos Trigonométricos
• Graficar Seno y Coseno con diferentes Coeficientes
• Valores Máximos y Mínimos de las Funciones Seno y Coseno
• Graficar Funciones Trigonométricas: Amplitud, Período, Desplazamiento Vertical y Horizontal
• Gráficos Tangentes, Cotangentes, Secantes, Cosecantes

Identidades trigonométricas

Este es el punto en el que las funciones trigonométricas cobran vida propia aparte de su base en relaciones laterales triangulares. Las funciones contienen numerosas identidades que iluminan la relación entre diferentes tipos de funciones trigonométricas.

Estas identidades se pueden usar para encontrar los valores de ángulos fuera de los ángulos de referencia comunes. De hecho, eran la principal herramienta disponible para hacer eso antes de las calculadoras.

Este tema explica las identidades trigonométricas y cómo encontrarlas y recordarlas. También explica cómo usar las identidades para simplificar expresiones, lo que implica una buena cantidad de manipulación algebraica.

La guía explica cómo encontrar los valores de diferentes ángulos basados en ángulos de referencia con las identidades de suma y diferencia y las fórmulas de doble ángulo y medio ángulo. El tema continúa y concluye con más formas de simplificar, factorizar y resolver ecuaciones trigonométricas.

• Identidades Trigonométricas
• Identidades Trigonométricas: Cómo Derivarlas/ Recordarlas
• Usando Identidades Trigonométricas para Simplificar Expresiones
• Identidades de Suma y Diferencia
• Fórmulas de Doble Ángulo y Medio Ángulo
• Ecuaciones Trigonométricas
• Simplificando Expresiones Trigonométricas Usando Identidades Trigonométricas
• Simplificando Expresiones Trigonométricas Que Involucran Fracciones
• Simplificando Productos de Binomios Que Involucran Funciones Trigonométricas
• Factorizando y Simplificando Expresiones Trigonométricas
• Resolver Ecuaciones Trigonométricas
• Resolver Ecuaciones Trigonométricas Usando Factorización
• Ejemplos con Funciones Trigonométricas: Par, Impar o Ninguna
• Demostrando una Identidad Trigonométrica