A háromszögek egyszerű számoknak tűnhetnek, de a mögöttük álló matematika elég mély ahhoz, hogy saját tárgyának lehessen tekinteni: trigonometria.

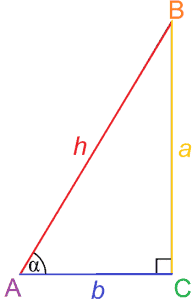
ahogy a neve is sugallja, a trigonometria a háromszögek tanulmányozása. Pontosabban, a trigonometria a háromszögek szögei és oldalai közötti kapcsolatokkal foglalkozik.

kissé meglepő módon a trigonometrikus arányok a körök gazdagabb megértését is biztosíthatják. Ezeket az arányokat gyakran használják a számításban, valamint számos tudományágban, beleértve a fizikát, a mérnöki munkát és a csillagászatot.

az útmutatóban található források a trigonometria alapjait fedik le, beleértve a trigonometrikus arányok és függvények meghatározását. Ezután áttekintik, hogyan használják ezeket a funkciókat a problémákban, és hogyan ábrázolják őket.

végül ez az erőforrás-útmutató a leggyakoribb trigonometrikus azonosságok magyarázatával zárul.

alapvető trigonometria

a trigonometria különösen a derékszögű háromszög oldalainak arányaival foglalkozik, amelyek felhasználhatók a szög mértékének meghatározására. Ezeket az arányokat trigonometrikus függvényeknek nevezzük, és a legalapvetőbbek a szinusz és a koszinusz.

Ez a két függvény a többi jól ismert trigonometrikus függvény meghatározására szolgál: tangens, secant, cosecant és cotangent.

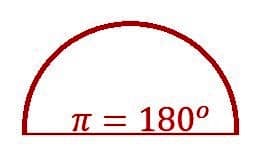
Ez a szakasz a derékszögű háromszögek áttekintésével és az alapvető trigonometrikus függvények ismertetésével kezdődik. Ez magyarázza a viszonosságukat is. A téma kiterjed a trigonometrikus szögek értékelésére is, különös tekintettel a 30, 45 és 60 fokos speciális szögekre.

végül a témakör útmutatója ismerteti, hogyan kell kezelni a trigonometrikus függvények inverzeit és a szögek mérésének két leggyakoribb módját.

• határozza meg a derékszögű háromszögek oldalait
• trigonometrikus függvények vagy Trig. Arányok
• szinusz
• koszinusz
• tangens
• szinusz, koszinusz és tangens áttekintése
• szekáns, koszekáns, kotangens
• Sin, Cos, Tan, Sec, Csc, Cot
• Társfunkciók
• trigonometrikus szögek értékelése
• speciális szögek: 30 fok, 45 fok, 60 fok
• számológép használata
• inverz trigonometria
• fok és radián

A trigonometria alkalmazásai

valójában sokféle elméleti és gyakorlati alkalmazás létezik a trigonometrikus funkciókhoz. Felhasználhatók hiányzó oldalak vagy szögek megtalálására egy háromszögben, de felhasználhatók a híd tartógerendáinak hosszának vagy egy magas tárgy magasságának az árnyék alapján történő megkeresésére is.

Ez a témakör a trigonometriai problémák különböző típusait tárgyalja, valamint azt, hogy az alapvető trigonometrikus függvények hogyan használhatók ismeretlen oldalhosszok keresésére. Azt is magában foglalja, hogyan lehet használni, hogy megtalálják szögek, sőt a terület egy háromszög.

végül ez a szakasz a szinuszok törvényeiről és a koszinuszok törvényéről szóló altémákkal zárul.

• trigonometriai problémák
• Szinuszproblémák
• Koszinuszproblémák
• tangens problémák
• keresse meg a derékszög ismeretlen oldalait
• keresse meg az objektum magasságát trigonometria segítségével
• trigonometriai Alkalmazások
• magasság és mélyedés szöge
• háromszög területe a szinusz függvény használatával
• szinuszok törvénye vagy szinusz szabály

/li>

• koszinusz törvény vagy koszinusz szabály

trigonometria a derékszögű síkban

a derékszögű síkban a trigonometria az egységkör körül helyezkedik el. Ez azt jelenti, hogy a kör középpontja a (0, 0) ponton 1 sugarú. Bármely vonal, amely összeköti az eredetet a kör egy pontjával, derékszögű háromszögként építhető fel, amelynek hossza 1. A háromszög lábainak hossza betekintést nyújt a trigonometrikus funkciókba. Az egységkör ciklikus jellege a grafikonhoz hasznos funkciók mintáit is feltárja.

Ez a témakör a standard helyzetben lévő szögek és a közös szögek leírásával kezdődik, mielőtt elmagyarázná az egységkört és a referenciaszögeket. Ezután bemutatja, hogyan változnak a trigonometrikus függvények értékei a derékszögű sík kvadránsának alapján. Végül ez a szakasz azzal zárul, hogy elmagyarázza, hogyan lehet az egységkört és az xy-síkot trigonometriai problémák megoldására használni.

• szögek Standard helyzetben és közös szögek
• egység kör
• Referenciaszög
• trigonometrikus arányok a négy kvadránsban
• annak a kvadránsnak a megkeresése, amelyben egy szög fekszik
• közös szögek
• trigonometrikus függvények a derékszögű síkban
• fokok és Radiánok
• trigonometrikus függvények kiértékelése egy szögre, adott pont a szög
• trigonometrikus függvények értékelése a Referenciaszög segítségével
• trigonometrikus értékek keresése adott trigonometrikus érték/egyéb információ
• trigonometrikus érték értékelése Függvények fontos szögekben

trigonometrikus függvények grafikonjai

bár a derékszögű síkban lévő egységkör trigonometrikus függvényeket biztosít, ezeknek a függvényeknek mindegyikének saját grafikonja is van. Ezek a Grafikonok ciklikus jellegűek. A trig függvények grafikonjai általában akkor a legértelmesebbek, ha az x tengelyt pi radiánok intervallumaira osztják, míg az y tengely még mindig egész számok intervallumaira oszlik.

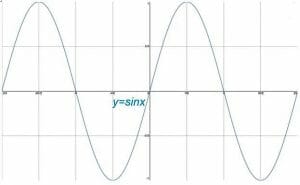
Ez a témakör a szinusz, koszinusz és tangens alapgráfjait tartalmazza. Ezután a gráfok transzformációit és azok tulajdonságait tárgyalja. Végül a téma egy altémával zárul le az alapvető trig függvények reciprokainak grafikonjairól.

• trigonometriai gráfok
• szinusz gráf
• koszinusz gráf
• tangens gráf
• trigonometrikus gráfok transzformációi
• szinusz és koszinusz ábrázolása különböző együtthatókkal
• szinusz és koszinusz függvények maximális és minimális értékei
• Trig függvények ábrázolása: Amplitúdó, periódus, függőleges és vízszintes eltolódások
• érintő, kotangens, szekáns, koszekáns gráfok

trigonometrikus azonosságok

Ez az a pont, ahol a trigonometrikus függvények önálló életet élnek, eltekintve a háromszög oldalarányainak alapjától. A függvények számos identitást tartalmaznak, amelyek megvilágítják a trig funkciók különböző típusai közötti kapcsolatot.

Ezek az identitások felhasználhatók a szögek értékeinek megkeresésére a közös referenciaszögeken kívül. Valójában ezek voltak a fő eszköz, amely a számológépek előtt elérhető volt.

Ez a téma elmagyarázza a trigonometrikus azonosságokat, és hogyan lehet megtalálni és megjegyezni őket. Azt is elmagyarázza, hogyan lehet az identitásokat a kifejezések egyszerűsítésére használni, ami elég sok algebrai manipulációt jelent.

Az útmutató elmagyarázza, hogyan lehet megtalálni a különböző szögek értékeit a referenciaszögek alapján az összeg és különbség identitásokkal, valamint a kettős és félszög képletekkel. A téma folytatódik és befejeződik a trigonometrikus egyenletek egyszerűsítésének, tényezőjének és megoldásának több módjával.

• trigonometrikus identitások
• trigonometrikus identitások: Hogyan lehet levezetni/ emlékezni rájuk
• trigonometrikus identitások használata a kifejezések egyszerűsítéséhez
• összeg és különbség identitások
• kettős szögű és Félszögű képletek
• trigonometrikus egyenletek
• trigonometrikus kifejezések egyszerűsítése Trig identitások használatával
• a törteket tartalmazó trigonometrikus kifejezések egyszerűsítése
• A trigonometrikus függvényeket tartalmazó binomiális termékek egyszerűsítése
• faktoring és a trigonometrikus kifejezések egyszerűsítése
• /li>
• trigonometrikus egyenletek megoldása
• trigonometrikus egyenletek megoldása faktoring segítségével
• példák trigonometrikus függvények: Páros, Páratlan, vagy sem
• bizonyítja a trigonometrikus azonosságot