Trójkąty mogą wydawać się prostymi figurami, ale matematyka za nimi jest na tyle głęboka, że można ją uznać za swój własny przedmiot: trygonometrię.

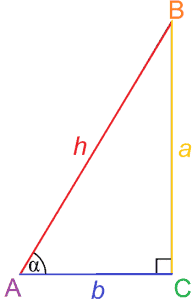
jak sama nazwa wskazuje, Trygonometria jest badaniem trójkątów. Dokładniej, Trygonometria zajmuje się związkami między kątami i bokami w trójkątach.

nieco zaskakująco, współczynniki trygonometryczne mogą również zapewnić bogatsze zrozumienie okręgów. Współczynniki te są często używane w rachunku różniczkowym, a także w wielu gałęziach nauki, w tym w fizyce, inżynierii i astronomii.

zasoby w tym przewodniku obejmują Podstawy trygonometrii, w tym definicję współczynników trygonometrycznych i funkcji. Następnie omawiają, jak korzystać z tych funkcji w problemach i jak je wykresować.

wreszcie, ten przewodnik zasobów kończy się wyjaśnieniem najczęstszych tożsamości trygonometrycznych.

Trygonometria Podstawowa

Trygonometria zajmuje się przede wszystkim współczynnikami boków trójkąta prostokątnego, które można wykorzystać do określenia miary kąta. Współczynniki te nazywane są funkcjami trygonometrycznymi, a najbardziej podstawowe to sinus i cosinus.

te dwie funkcje są używane do zdefiniowania innych znanych funkcji trygonometrycznych: tangent, secant, cosecant i cotangent.

Ta sekcja zaczyna się od przeglądu trójkątów prostokątnych i wyjaśnienia podstawowych funkcji trygonometrycznych. Wyjaśnia również ich wzajemność. Temat obejmuje również sposób oceny kątów trygonometrycznych, w szczególności kątów specjalnych 30-, 45-i 60-stopni.

wreszcie, przewodnik po tym temacie obejmuje jak radzić sobie z odwrotnością funkcji trygonometrycznych i dwa najczęstsze sposoby mierzenia kątów.

• Zidentyfikuj boki trójkątów prostokątnych
• funkcje trygonometryczne lub trygonometryczne. Współczynniki
• Sinus
• Cosinus
• tangens
• przegląd sinusa, cosinusa i tangensa
• Secant, Cosecant, Cotangent
• Sin, Cos, Tan, sec, Csc, Cot
• funkcje współdzielone
• obliczają Kąty trygonometryczne
• Kąty specjalne: 30-stopni, 45-stopni, 60-stopni
• Korzystanie z kalkulatora
• Trygonometria odwrotna
• stopnie i radiany

zastosowania trygonometrii

istnieje wiele różnych teoretycznych i praktycznych zastosowań funkcji trygonometrycznych. Mogą być używane do znajdowania brakujących boków lub kątów w trójkącie, ale mogą być również używane do znajdowania długości belek nośnych mostu lub wysokości wysokiego obiektu opartego na cieniu.

ten temat obejmuje różne rodzaje problemów z trygonometrią i jak podstawowe funkcje trygonometryczne mogą być używane do znajdowania nieznanych długości boku. Obejmuje również sposób, w jaki można je wykorzystać do znajdowania kątów, a nawet powierzchni trójkąta.

W końcu ten rozdział kończy się podtytułami dotyczącymi praw sinusów i praw cosinusów.

• problemy z trygonometrią
• problemy z sinusem
• problemy z Cosinusem
• problemy styczne
• Znajdź nieznane boki kątów prostych
• Znajdź wysokość obiektu za pomocą trygonometrii
• Aplikacje trygonometryczne
• kąt podniesienia i obniżenia
• obszar trójkąta za pomocą funkcji sinus
• prawo sinus lub reguła Sinus/li>
• prawo cosinusów lub reguła cosinusów

Trygonometria na płaszczyźnie kartezjańskiej

Trygonometria na płaszczyźnie kartezjańskiej jest wyśrodkowana wokół okręgu jednostkowego. Oznacza to, że okrąg wyśrodkowany w punkcie (0, 0) o promieniu 1. Każda linia łącząca początek z punktem na okręgu może być skonstruowana jako trójkąt prostokątny z przeciwprostokątną o długości 1. Długości nóg trójkąta zapewniają wgląd w funkcje trygonometryczne. Cykliczny charakter okręgu jednostkowego ujawnia również wzory w funkcjach przydatnych do Wykresów.

ten temat zaczyna się od opisu kątów w położeniu standardowym i kątów koterminalnych przed wyjaśnieniem okręgu jednostkowego i kątów odniesienia. Następnie opisuje, jak zmieniają się wartości funkcji trygonometrycznych w oparciu o kwadrant płaszczyzny kartezjańskiej. Na koniec Ta sekcja kończy się wyjaśnieniem, w jaki sposób okrąg jednostkowy i płaszczyzna xy mogą być użyte do rozwiązywania problemów trygonometrii.

• kąty w położeniu standardowym i kąty Koterminalne
• okrąg jednostkowy
• kąt odniesienia
• współczynniki trygonometryczne w czterech ćwiartkach
• znalezienie kwadrantu, w którym leży kąt
• Kąty Koterminalne
• funkcje trygonometryczne na płaszczyźnie kartezjańskiej
• stopnie i radiany
• obliczanie funkcji trygonometrycznych dla kątów, biorąc pod uwagę punkt na kąt
• obliczanie funkcji trygonometrycznych za pomocą kąta odniesienia
• znajdowanie wartości trygonometrycznych podanej jednej wartości trygonometrycznej/inne info
• Obliczanie trygonometrycznych Funkcje pod ważnymi kątami

wykresy funkcji trygonometrycznych

chociaż okrąg jednostkowy na płaszczyźnie kartezjańskiej dzieli się na funkcje trygonometryczne, każda z tych funkcji ma również swój własny wykres. Wykresy te mają charakter cykliczny. Zazwyczaj wykresy funkcji trygonometrycznych mają największy sens, gdy oś x jest podzielona na interwały pi radianów, podczas gdy oś y jest nadal podzielona na interwały liczb całkowitych.

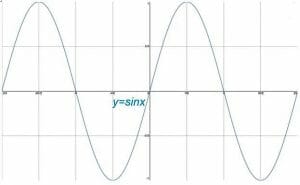
ten temat obejmuje podstawowe wykresy sinusa, cosinusa i stycznej. Następnie omawia przekształcenia tych wykresów i ich właściwości. Na koniec temat kończy się subtopią o grafach odwrotności podstawowych funkcji trygonometrycznych.

• wykresy trygonometryczne
• Wykres sinusoidalny
• Wykres Cosinus
• Wykres styczny
• transformacje Wykresów trygonometrycznych
• wykresy sinusoidalne i cosinus o różnych współczynnikach
• maksymalne i minimalne wartości funkcji sinusoidalnych i cosinus
• wykresy trygonometryczne: Amplituda, okres, Pionowe I Poziome przesunięcia
• tangens, Cotangent, Secant, Cosecant wykresy

tożsamości trygonometryczne

jest to punkt, w którym funkcje trygonometryczne przyjmują własne życie, niezależnie od ich podstawy w współczynnikach boku trójkąta. Funkcje zawierają liczne tożsamości, które oświetlają relacje między różnymi rodzajami funkcji trygonometrycznych.

tożsamości te mogą być użyte do znalezienia wartości kątów poza wspólnymi kątami odniesienia. W rzeczywistości były one głównym narzędziem dostępnym do robienia tego przed kalkulatorami.

ten temat wyjaśnia tożsamości trygonometryczne oraz jak je znaleźć i zapamiętać. Wyjaśnia również, jak używać tożsamości do upraszczania wyrażeń, co wymaga sporej ilości manipulacji algebraicznych.

przewodnik wyjaśnia, jak znaleźć wartości różnych kątów na podstawie kątów odniesienia z tożsamościami sumy i różnicy oraz formułami podwójnego kąta i pół kąta. Temat kontynuuje i kończy się kolejnymi sposobami upraszczania, dzielenia i rozwiązywania równań trygonometrycznych.

• tożsamości trygonometryczne
• tożsamości trygonometryczne:
• używanie tożsamości trygonometrycznych do upraszczania wyrażeń
• tożsamości sumy i różnicy
• wzory dwu-i pół-kątowe
• równania trygonometryczne
• upraszczanie wyrażeń trygonometrycznych przy użyciu tożsamości trygonometrycznych
• upraszczanie wyrażeń trygonometrycznych z udziałem ułamków
• upraszczanie produktów Dwumianów z udziałem funkcji trygonometrycznych
• Faktorowanie i upraszczanie wyrażeń trygonometrycznych
• Rozwiązywanie równań trygonometrycznych
• Rozwiązywanie równań trygonometrycznych za pomocą faktoringu
• przykłady z funkcjami Trygonometrycznymi: parzystymi, nieparzystymi lub nieparzystymi
• dowodząc tożsamością trygonometryczną